下記の記事はPET基材P-Flex® について書かれています。2018年7月2日よりポリイミド基材 P-Flex® の製造販売開始いたしました。
詳しくはこちらをご覧ください。

【フレキシブル基板を科学する!シリーズ ライター自己紹介】
筑波大学・修士1年。
デジタルファブリケーションに関する研究をしている。
ディズニー映画とディズニーランドとディズニー音楽が大好き。
将来の夢は、ディズニー映画のエンドロールに自分の名前がのることです。
<< 前の記事
こんにちは!学生ライターの小池です。
普段は情報系の大学院で、3Dプリンタを使った研究をしています。
P-Flex®で製造・販売するフィルムが薄くなったことに関連して、なぜ基板が薄いといいのか?
そのメリットについて材料力学的に解説していく【フレキシブル基板を科学する!】シリーズですが、
前回のブログでは、曲げ剛性という観点から基板が薄いことによるメリットについて解説しました。
【フレキシブル基板を科学する! 前編】基板が薄いことによるメリットとは? 〜曲げ剛性編〜 – エレファンテック 技術ブログ
【後編】では耐屈曲性という観点からお話しします。
☆ 今回のブログのポイント☆
- 板の屈曲に対する耐久性を表す概念として「耐屈曲性」がある。
- 「耐屈曲性」はいわば、フレキシブル基板が断線するまでの寿命である。
- 寿命を伸ばすには、できるだけ1回の屈曲あたりに基板にかかる負担(=縁応力)を少なくしてあげれば良い。
- 曲げる方向に対して板を薄くすると縁応力値が小さくなり、「耐屈曲性」が上がる。
フレキシブル基板の用途と耐屈曲性
フレキシブル基板には用途により、以下の2種類の配線方法があります。
- 機器への接続後に動かすことはない、固定配線
- ヒンジ部*1などに使用され繰り返し屈曲する、可動部配線
2.のようなヒンジ部に使用される可動部配線の場合、繰り返し屈曲が起こります。
「薄くて柔軟性があること」こそがフレキシブル基板の醍醐味でありますが、
屈曲を繰り返せば回路は疲労し、いつかはヒビが入りやがて断線してしまいます。
せっかく電子辞書を買っても、数回開けただけで壊れてしまったら、悲しいですよね?
そこで「耐屈曲性」の性能をあげて、できるだけフレキシブル基板の寿命を伸ばしてあげることが、
繰り返し屈曲するような製品を作る上で非常に重要なのです。
さて!この「耐屈曲性」ですが、フレキシブル基板の厚さが薄くなることで、この性能が上がります。
というわけで、今回のブログでは、なぜ薄いと「耐屈曲性」が上がるのか材料力学的に解説します!
ここからは、下図のような厚みh、幅b、長さI の板をθ度曲げることを前提に、図の簡易化のため青色の面を使って解説します
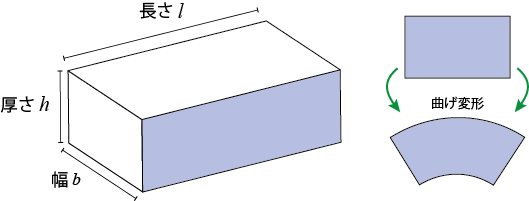
耐屈曲性を語るにあたって、縁応力を考えます
それは、縁応力が屈曲した際に板にかかる負担そのものだからです。
板を曲げると、以下の図のように中立面*2(黄)を境に、引っ張り力(赤)と圧縮力(青)がかかります。
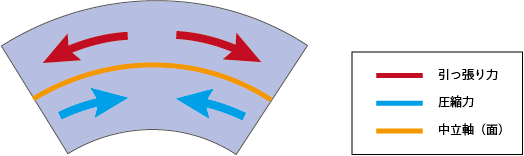
この2種類の力ですが、曲げ変形の場合は断面に均一にかかりません。
以下のように、中立面に近づくほど応力*3が小さく、離れるほど大きくなります。
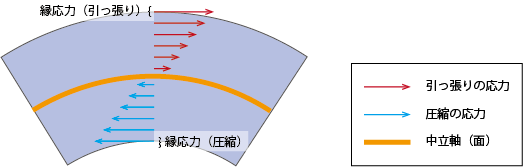
つまり、応力が最大になる地点は、板の上端と下端です。
この端っこにかかる応力を縁応力(ふちおうりょく)と呼びます。
この2つの縁応力のうち、引っ張るほうの縁応力が
フレキシブル基板の屈曲において断線の原因となるのです。
なぜ、縁応力が断線の原因になるの?
ではなぜ縁応力が断線の原因になるのでしょうか?
ここで下の図のようなたい焼きを半分こする時のことを考えて見てほしいのですが、
緑の矢印の方向に力を入れた際に、一番はしっこ(★の部分)から紫の矢印の方向へ割れていくと思います。
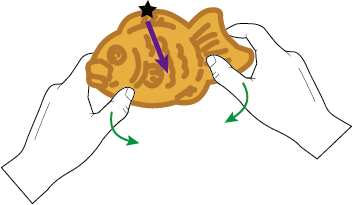
決してたい焼きのお腹から破けたりしませんよね。
繰り返しの屈曲で断線してしまうフレキシブル基板もたい焼きを半分こするときと同じで、
引っ張りの力がかかっている一番端の部分から、クラックが入り壊れていくのです。
これが、縁応力(=最端にかかる引っ張り応力)が断線の原因になる理由です。
縁応力と板の厚みの関係
ここまでで、一番端の部分にかかる負担を少なくする(=引っ張る縁応力を抑える)ことで、
基板が壊れにくくなるということがわかっていただけたと思います。
縁応力σmaxは板を曲げた時に生じる歪みから、
フックの法則を用いて以下のように求めることができます。
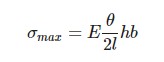
上記から、厚さhが小さいほど、応力が小さくなるという、縁応力と板の厚みの関係がわかると思います!
つまり同じヤング率Eの素材で、同じ幅b・同じ長さl の板をθ度曲げる場合、
厚さhが小さいほど、応力が小さくなり屈曲の際の負担が少なくなるので、耐屈曲性が上がるのです!!
細かい式変形は、おまけを参照してみてください☆
まとめ
耐屈曲性と基板の厚さの関係について、理解していただけたでしょうか?
薄い板の方が分厚いものよりも、一回の屈曲に対する板への負担が少ないため
なんども屈曲を繰り返すことができる(=寿命が長い)という内容でした。
世界ではじめての図書館(アッシュールバニパルの図書館)の資料は、全て粘土板だったそうです。
そのうち図書館の資料は、羊皮紙を使った巻子本(巻物)になるのですが、
その当時、羊皮紙職人が動物の皮を頑張って薄くしていたそうです。
当時の人は「記録媒体が薄いと丸められるし、持ち運びできるし何度も開閉できるから超便利じゃん!」
なんてテンションが上がったんじゃないかなあと思いました。
おまけ
今回のブログでは、最大応力の式をお見せしましたが、
なんとなくしっくりきていない方も多いかと思います。
なぜなら、最大応力を求めるまでの式変形の部分を大幅に省いたからです!!!!!!!!!!!
このおまけ部分では、最大応力を求めるまでの式変形を解説したいと思います。
まず以下のように、厚さh、幅がb、長さがlの板を θ曲げる場合に生じる歪みについて考えてみます。
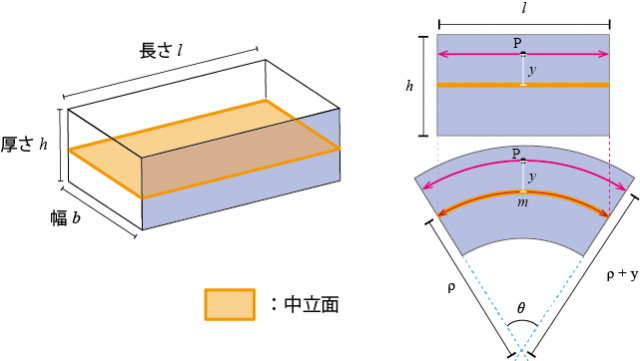
上図、右側の黄色い線は中立面の長さを表しています。
点 P を通る面での長さ変化量Δxについてまずは考えてみましょう!
上図で、右側の板を曲げる前と後でピンク色の線の長さがどれくらい変わったかが変化量Δxです。
曲率半径をρとすると、変形後に点 P を通る面の長さは、 (ρ + y)θ と表すことができますね。*4
よって、θ度、板を屈曲させた時の変化量Δxは、変形後に点 P を通る面の長さから、
変形前の長さ l の差をとって以下のようになります。
Δx = (ρ + y)θ – l
Δx = (ρθ + yθ) – l
ここで、m = ρθと m ≒ l より、*5
Δx = yθ
以上により、中立面から y離れた P 地点を通る面の長さの変化量がわかったので、
P 地点での曲げた後の歪みは以下のように表すことができます。

このおまけでは本文で省略してしまった、式変形の部分を解説しました。
ただ板を曲げるだけでも厚みだけでなく、
色々なパラメータが関わっていることにも気づいていただけたと思います!
私は、この記事を書くために材料力学の勉強をしていますが、
パラメータがたくさん出てくると、よく頭がこんがらがってしまいます(泣)
でも、悪戦苦闘しながらとっても楽しく記事を書いています!
今後もじゃんじゃんフレキシブル基板を科学していきたいと思います!
このブログで紹介・解説したことで、みなさんの生活や開発に少しでもお役に立てていたら嬉しいです(^^)
